Python. Бинарный поиск в массиве

В этой статье мы рассмотрим Двоичный (бинарный) поиск - один из классических алгоритмов поиска элемента в отсортированном массиве.

Предположим вы знаете в каком месяце родился ваш друг(пусть это будет сентябрь) , но не знаете в какой день. И вам нужно за наименьшее количество попыток определить в какой день месяца он родился. И при этом вам ваш друг на каждую вашу попытку будет давать один их трех ответов: "мало", "много" или "угадал"

Самый простой способ это метод простого поиска. Вы перебираете все варианты подряд 1, 2, 3 и далее.Конечно , если ваш друг родился 3 сентября вам понадятся всего лишь три попытки , но если 24 сентября , то вам нужно 24 попытки. А если друг родился 30 сентября , то нужны все 30 попыток.

Рассмотрим другой более эффективный метод поиска.

Допустим , что у нашего друга день рождения 24 сентября. Так как исходный массив содержит 30 элементов , то мы на первом шаге назовем элемент который находится посередине этого массива. Это число 15. Наш друг говорит , что "мало". И теперь мы понимаем , что все числа меньше 15 и само число 15 можно исключить из поиска и можно сосредоточиться на числах, которые больше 15.

На втором шаге мы назовем число которое находится посередине чисел от 16 до 30 и этим числом является 23 , но это тоже меньше искомого числа. И поэтому мы исключаем все числа меньше 23 и само число 23.

И так мы повторяем пока не найдем искомое число.В нашем случае это число 24.

Ниже на рисунке для наглядности показаны все шаги нахождения искомого числа(число 24) методом бинарного поиска

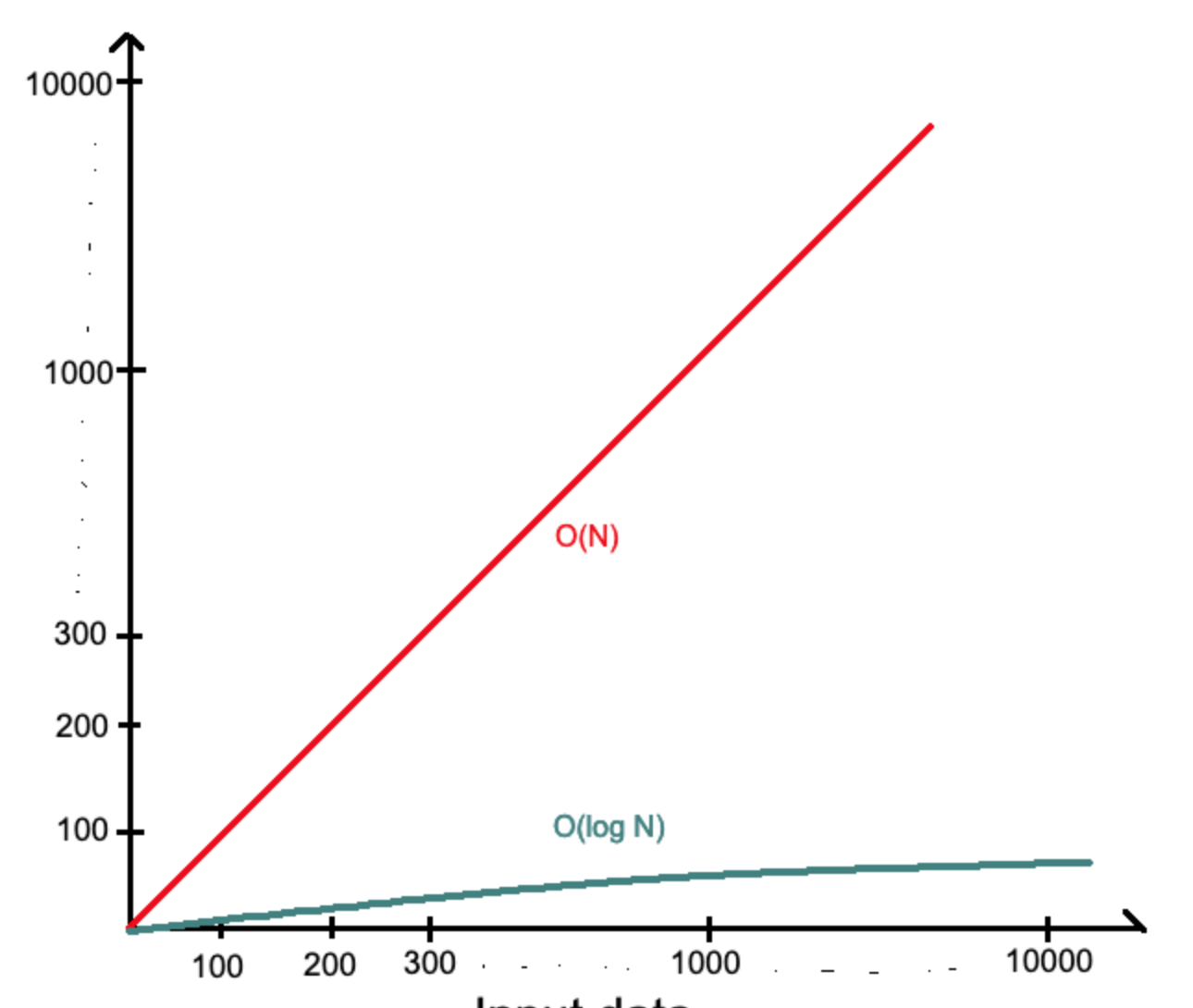
Чтобы найти число 24 в массиве из 30 элементов при помощи простого поиска нам нужно 24 попытки , то при помощи бинарного поиска нам потребовалось всего лишь 5 попыток. То есть в массиве из 30 элементов мы гарантированно за 5 попыток можем найти любой элемент, так log 30 примерно будет равно 5.

А что будет если у нас количество элементов равно не 30 , а скажем 1000? То тогда при простом поиске(переборе) , чтобы найти число 1000 нужно сделать 1000 итераций(попыток). А вот при бинарном поиске нужно сделать всего лишь 10 попыток , потому что 2 в 10 степени это 1024. Для 10 тысячи элементов при бинарном поиске нужно всего лишь 14 попыток , а вот при переборе количество попыток растет линейно. В этом и мощь бинарного алгоритма и его широкое распространение.

O(log n) — логарифмическая сложность для бинарного поиска

O(n) — Линейная сложность для простого поиска

Сравнение линейной и логарифмической функций.

Реализация алгоритма бинарного поиска на Python.

def binary_search(sequence, start_element, key):
    end_element = len(sequence) - 1
    while start_element <= end_element:
        middle_element = start_element + (end_element - start_element) // 2
        if sequence[middle_element] == key:
            return middle_element
        elif sequence[middle_element] < key:
            start_element = middle_element + 1
        else:
            end_element = middle_element - 1
    return -1


# Можно было еще элегантно создать sequence = [i for i range(1, 31)],
# но для наглядности перечислил все элементы
sequence = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
            11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
            21, 22, 23, 24, 25, 26, 27, 28, 29, 30]
# Число которое мы ищем
find_element = 24

result = binary_search(sequence=sequence, start_element=0, key=find_element)
print(result)

Заключение

В данной статье мы рассмотрели один из классических алгоритмов поиска. Это бинарный поиск элемента в отсортированном массиве.